Step-by-step explanation
We are asked to find the value of v and w
To do so, we will make use of trigonometric identities
Let us get the value of v first
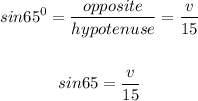
cross multiply to get v
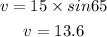
The value of v is 13.6
Next, we will get w

The value of w is 40.4 degrees