Since the current solution is 95% alcohol, then the amount of alcohol present is:
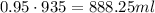
Let 'x' be the amount of water that we will add to our soulution. Then, the new amount of liquitd would be 935ml + x or 935 + x
We want a solution that is 85% alcohol, so, we have the following equation:
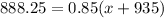
solving for 'x', we get:
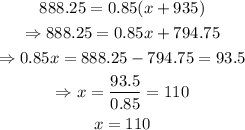
Since x = 110, this means that we will have the following:
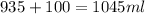
ttherefore, you will need 110ml of pure water to obtain 1045ml of the desired 85% solution