Question

For ABC, let a = 10 , b = 18, and c = 13......

Answer 1

Since the three sides of the triangle are given, to get the measure of an angle in the triangle, we can use Cosine Law.

To find the measure of Angle C using Cosine Law, here is the formula:

`\cos C=(a^2+b^2-c^2)/(2ab)`

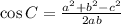
Let's plug in those given information in the question to the formula above.

`\cos C=(10^2+18^2-13^2)/(2(10)(18))`

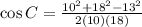
Then, solve.

`\begin{gathered} \cos C=(100+324-169)/(360) \\ \cos C=(255)/(360) \\ C=\cos ^(-1)(255)/(360) \\ C=44.9 \end{gathered}`

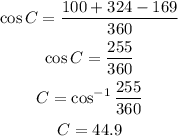
Therefore, the measure of angle C is 44.9°. (Option D)