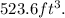Question

The surface area of a sphere is 314.16 ft squared. What is the volume?

Answer 1

To solve this problem, we will determine the radius of the sphere using the formula for the SA, then we will use the radius to compute the volume of the sphere. ( We will omit the units to simplify the calculations).

The formula for the surface area of a sphere is:

`SA=4\pi r^2,`

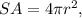
where r is the radius of the sphere. Therefore,

`314.16=4\pi r^2.`

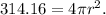
Solving the above equation for r, we get:

`\begin{gathered} (314.16)/(4\pi)=r^2, \\ \sqrt{(314.16)/(4\pi)}=r. \end{gathered}`

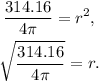
Therefore, the radius of the sphere is:

`r\approx5\text{ ft.}`

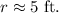
Now, the volume of a sphere is given by the following formula:

`V=(4)/(3)\pi r^3.`

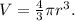
Substituting the above value, we get:

`V\approx523.6\text{ ft}^3.`

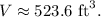
Answer:

`523.6ft^3.`