Question

Hi there! I need help understanding the following graph question. y=2 * 1/2. the number 1/2 has what looks like a letter exponent above the one. Please zoom attached picture. The answer is A not the circled answer. Does it apply to the formula y=mx+b?

Answer 1

Given the following exponential equation:

`y=2\cdot((1)/(2))^x`

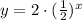
For x = 0, we have:

`y=2\cdot((1)/(2))^0=2\cdot1=2`

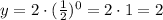
Then, the y-intercept must be y = 2. Now, for x = -2:

`y=2\cdot((1)/(2)){}^(-2)=2\cdot(2)^2=2\cdot4=8`

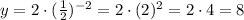
Looking at D, we see that the y-intercept is 4, so this graph does not correspond to the equation. Looking at B and C, we see that y ≠ 8 for x = -2, so we discard them.

For A:

We see that y = 8 for x = -2, and the y-intercept is 2. Then, this is the corresponding graph of the equation.

Answer: A