In order to describe the dimensional formula of this coefficient, first let's write the formula for the friction force:
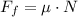
Where Ff is the friction force (in Newtons), μ is the friction coefficient and N is the normal force (in Newtons).
Changing each variable to its corresponding unit (except for the coefficient), we have:
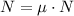
Solving for μ, we have:
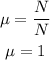
Since μ = 1, that means it has no dimensions, it's only a constant value (it is an adimensional value).