Question

Find the sum of a 10-term geometric sequence when the first term is 3 and the last term is 59,049 and select the correct answer below.

Answer 1

Given:

geometric series

number of terms (n) = 10

first term (a₁) = 3

tenth term (a₁₀) = 59, 049

Find: sum of the geometric sequence

Solution:

The formula for the sum of the geometric sequence is:

`S=(a_1(1-r^n))/(1-r)`

From the formula, we need the first term, ratio, and the number of terms. However, based on the given information, we don't have the value of ratio (r) yet. To solve for the ratio, we have the formula below:

`lastterm=firstterm(r)^(n-1)`

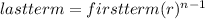
Let's plug in the given data to solve for the ratio first.

`\begin{gathered} 59,049=3r^(10-1) \\ 59,049=3r^9 \\ \text{Divide both sides by 3.} \\ 19683=r^9 \\ \text{Get the third root.} \\ \sqrt[3]{19683}=\sqrt[3]{r^9} \\ 27=r^3 \\ \text{Get the third root again.} \\ \sqrt[3]{27}=\sqrt[3]{r^3} \\ 3=r \end{gathered}`

Therefore, the ratio for this geometric sequence is 3.

Now that we have the value of ratio, we can now solve for the sum of the geometric series.

`S=(a_1(1-r^n))/(1-r)`

Let's plug in the data that we have to the formula above.

`S=(3(1-3^(10)))/(1-3)=(3(1-59049))/(-2)=(-177144)/(-2)=88,572`

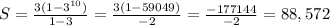
The sum of the 10-term geometric sequence is 88,572.