Question

A cart moving at 4 m/s bounces elastically off of a second cart of twice the mass which is moving at 2 m/s in the same direction. What velocity does each cart now have?

Answer 1

Given,

The velocity of teh 1st cart, u₁=4 m/s

The velocity of the s2nd cart, u₂=2 m/s

The mass of each cart is the same. Let us assume that the mass is 'm'

The elastic collision is the collision in which the total kinetic energy of a system is conserved. That is the total kinetic energy of the carts before the collision is equal to that after the collision.

The speed of the 1st cart after the collision, as it is the elastic collision, is given by,

`v_1=(m_1-m_2)/(m_1+m_2)u_1+(2m_2)/(m_1+m_2)u_2`

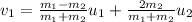
Where m₁ and m₂ are the mass of each cart. But in this case, the mass of both carts is the same.

Thus,

`\begin{gathered} v_1=\frac{m_{}-m_{}}{m+m}u_1+(2m)/(m+m)u_2 \\ =0+(2m)/(2m)u_2 \\ =u_2 \end{gathered}`

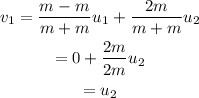
Thus the mass of the 1st cart after the collision is 2 m/s

Similarly, the velocity of the second craft, as this is an elastic collision, is

`\begin{gathered} v_2=(2m_1)/(m_1+m_2)u_1+(m_2-m_1)/(m_1+m_2)u_2 \\ =\frac{2m_{}}{m+m}u_1+(m-m)/(m+m)u_2 \\ =(2m)/(2m)u_1+0 \\ =u_1 \end{gathered}`

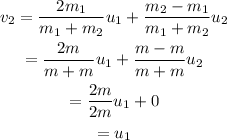
Thus the velocity of the second cart after the collision is 4 m/s