ANSWER
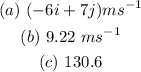
Step-by-step explanation
(a) To find the velocity of B relative to A, we have to find the vector subtraction of vectors B and A.
Hence, the velocity of B relative to A is:
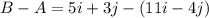
Simplify the expression:
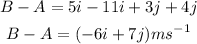
That is the velocity of B relative to A.
(b) To find the magnitude of the velocity of B relative to A, apply the formula for the magnitude of a vector:
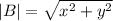
where (x, y) represents the coordinates of the vector
Hence, the magnitude of the velocity of B relative to A is:
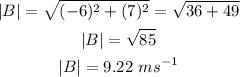
(c) To find the direction of the velocity of B relative to A, apply the formula for the direction of a vector:
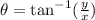
Hence, the direction of the velocity of B relative to A, as an angle from the positive x-axis is:
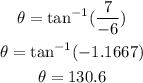
That is the answer.