Question

Which equation best fits the data in the table?A. y=1040(2)^xB. y=1040(1/2)^xC. y=520(1/2)^xD. y=1/2(1040)^x

Answer 1

`B\text{.}y=1040((1)/(2))^x`

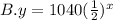
Step-by-step explanation:

On observation, the data on the table represents an exponential function.

An exponential function is a function of the form:

`y=ab^x`

When the number of hours, x=0

The number of parasites, y =1,040

`\begin{gathered} 1040=a* b^0 \\ \implies a=1,040 \end{gathered}`

When the number of hours, x=1

The number of parasites, y =520

`\begin{gathered} 520=1,040* b^1 \\ b=(520)/(1040) \\ b=(1)/(2) \end{gathered}`

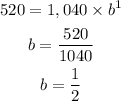
Thus, the equation that best fits the table is:

`y=1040\mleft((1)/(2)\mright)^x`

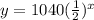
The correct choice is B.