The given sequence is :
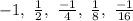
Geometric Sequence : A geometric sequence, is a sequence of non-zero numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio.
The expression is :
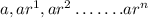
Common Ratio : A geometric sequence is one in which any term divided by the previous term is a constant. This constant is called the common ratio of the sequence
In the given sequence :
First term = (-1)
Second Term = (1/2)
Ratio of the second term to the first term :

Common Ratio = (-0.5)
The expression for the n-terms of Geometric sequence is :
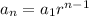
In the given system , first term = (-1) and the ratio r = (-1/2)
for 11 term, put n = 11
Substitute the value and simplify:
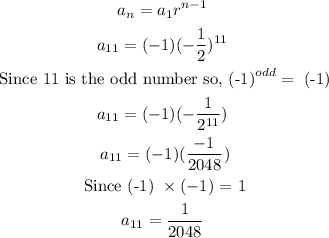
So, The 11 term is 1/2048
Answer : Common Ratio = (-0.5), 11 term is 1/2048