Question

The base of a triangle is (4x) m, and the height is (2x + 5) m. Findthe area of the triangle in terms of the variable x

Answer 1

As given by the question

There are given that the base of the triangle is (4x) and the height is (2x+5).

Now,

From the formula of area of a triangle;

`\text{Area of triangle=}\frac{\text{1}}{2}* base* height`

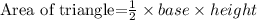
Then,

Put the both value into the above formula

So,

`\begin{gathered} \text{Area of triangle=}\frac{\text{1}}{2}* base* height \\ \text{Area of triangle=}\frac{\text{1}}{2}*4x*(2x+5) \\ \text{Area of triangle=}\frac{\text{1}}{2}*4x(2x+5) \end{gathered}`

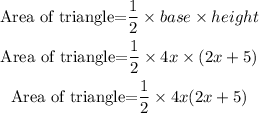
Then,

`\begin{gathered} \text{Area of triangle=}\frac{\text{1}}{2}*4x(2x+5) \\ \text{Area of triangle=}\frac{\text{1}}{2}*(8x^2+20x) \\ \text{Area of triangle=}((8x^2+20x))/(2) \\ \text{Area of triangle=}4x^2+10x \end{gathered}`

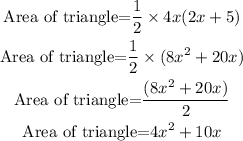
Hence, the area of a triangle is shown below:

`\text{Area of triangle=4x}^2+10x`