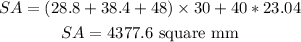Question

his figure is the pre-image of a prism that has undergone a dilation with a scale factor of 6/5.What is the surface area of the image after the dilation?2533 1/3 mm²3916 4/5 mm²4377 3/5 mm²5253 3/25 mm²

Answer 1

`SA=4377\text{ 3/5 mm}^2`

Explanation:

As a first step find the length of the sides after the dilation of 6/5.

The total surface area of a triangular prism is represented by the following equation;

`SA=(Perimeter*length)+(2*basearea)`

Therefore,

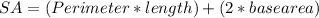
`SA=(28.8+38.4+48)*30+40*altitude`

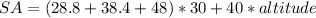
The missing altitude is given as:

`\begin{gathered} \frac{hypotenuse}{leg\text{ 1}}=\frac{leg\text{ 1}}{part\text{ 1}} \\ (48)/(28.8)=\frac{28.8}{part\text{ 1}} \\ part1=(28.8*28.8)/(48) \\ part1=(829.44)/(48) \\ part1=17.28 \end{gathered}`

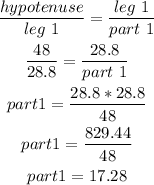
Now, use the Pythagorean theorem to find the altitude using part 1 of the hypotenuse:

`\begin{gathered} altitude=√(28.8^2-17.28^2) \\ altitude=23.04\text{ mm} \end{gathered}`

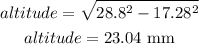
Hence, solve for the total surface area:

`\begin{gathered} SA=(28.8+38.4+48)*30+40*23.04 \\ SA=4377.6\text{ square mm} \end{gathered}`