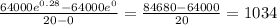Question

The population in a certain city was 64,000 in 2000, and its future size is predicted to be P(t)=64,000e0.014t, where t is the number of years after 2000.Complete parts a through d below.

Answer 1

So,

Here we have the following function:

`P(t)=64000e^(0.014t)`

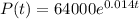
We want to know if the model indicates that the population is increasing or decreasing.

For this, if we graph, we would obtain something like:

So, the population is clearly increasing.

Suppose we want to know the population in 2002. So, remember that 2002 is two years after 2000, now we're going to replace t=2 in the equation:

`\begin{gathered} P(2)=64000e^(0.014(2)) \\ P(2)=64000e^(0.028) \\ P(2)=65817.32 \end{gathered}`

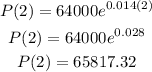
In 2020,

`\begin{gathered} P(20)=64000e^(0.28) \\ P(20)=84680 \end{gathered}`

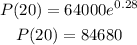
The average rate of growth:

`(64000e^(0.28)-64000e^0)/(20-0)=(84680-64000)/(20)=1034`