The data set is:
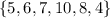
a) The variance of a data set is given by the formula:
![s^2=(1)/(N-1)\sum ^N_(n\mathop=1)(a_n-\operatorname{mean})^2]()
Where s^2 is the variance and P(a_n) is the probability of the value a_n.
First, we need to calculate the mean of the data set:
![\operatorname{mean}=((5+6+9+10+8+4))/(6)=(42)/(6)=7]()
Now, the variance is:
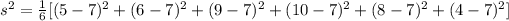
Then,

Therefore, the variance is equal to 5.6
b) As for the standard deviation, we simply need to get the square root of the variance. Then,
![\text{Standard deviation}=\sqrt[]{s^2}=\sqrt[]{5.6}\approx2.3664](https://img.qammunity.org/2023/formulas/mathematics/college/oq2keldka72fzpwjwh6k4gmi84mrn4v2qa.png)
The standard deviation is 2.3664 approximately