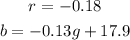Question

Find the correlation coefficient and the equation of the line of best fit for the data. Treat the number of girls in the class as the independent variable.

Answer 1

Let's find the correlation between the girls and the boys in a class, let's first just rewrite the data to make things easier, we know that girls are the independent variable then let's call it x, and the boys will be y. Then

y - boys

x - girls

To find the correlation we will use the following definition:

`r=\frac{\sum(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum(x_i-\bar{x})^2\cdot\sum(y_i-\bar{y})^2}}`

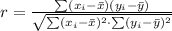
Now let's evaluate the mean of x, y, and all the necessary sums:

`\begin{gathered} \bar{x}=(\sum x_i)/(n)=17.5555555556 \\ \\ \bar{y}=(\sum y_i)/(n)=15.5555555556 \end{gathered}`

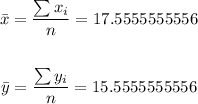
And the sums

`\begin{gathered} \sum(x_i-\bar{x})(y_i-\bar{y})=−88.77 \\ \\ \end{gathered}`

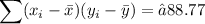
And the other sums:

Therefore the correlation will be

`\begin{gathered} r=(-88.77)/(√(674.22\cdot342.22)) \\ \\ r=-0.185 \end{gathered}`

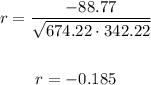
Now let's find the line that best fits the data, to do so let's use the following definitions for slope and y-intercept:

`\begin{gathered} m=\frac{\sum(x_i-\bar{x})(y_i-\bar{y})}{\sum(x_i-\bar{x})^2} \\ \\ b=\bar{y}-m\bar{x} \end{gathered}`

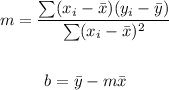
Then let's find the slope using the sums we have already calculated

`m=(-88.77)/(674.22)=-0.13`

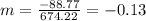
And the y-intercept

`\begin{gathered} b=15.55-(-0.13)\cdot(17.55) \\ \\ b=17.8 \end{gathered}`

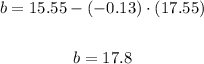
Therefore the line that best fit is

`y=-0.13x+17.9`

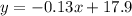
Final answer:

`\begin{gathered} r=-0.18 \\ b=-0.13g+17.9 \end{gathered}`