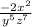Answer:
Simplifying the given expression using only positive exponents will give;
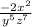
Step-by-step explanation:
Given the expression;
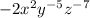
We want to re-write the expression such that it has only positive exponents.
Recall that;
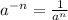
Re-writing the given expression, we have;
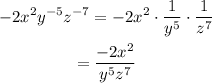
Therefore, simplifying the given expression using only positive exponents will give;