To compute the slope, intercept, and equation to predict the Price, we will use the formulae below:
For the equation
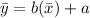
For the slope
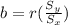
For the intercept
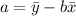
In this case, we have the following data given:
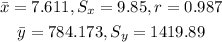
Part A
Upon substituting the above into the formula, we will have
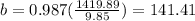
Hence slope = 141.41
Part B
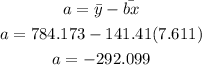
Hence, Intercept =-292.099
PART C
The equation that can be used to predict Price from Capacity
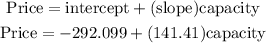
Therefore, the equation is
Price=-292.099+(141.41)capacity
Part D
To predict the price of a 20.0TB disk, we will simply set the capacity= to 20 and then simplify
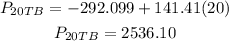
Hence, the predicted price is=2536.10