Answer:
10, 16, 22
Step-by-step explanation:
Pre-Solving
We are given an arithmetic sequence, and we already know that the first two terms are -2 and 4.
We want to find the next three terms in the sequence.
Solving
The formula for determining the nth term of an arithmetic sequence is
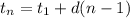 , where
, where
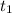 is the first term and d is known as the common difference.
is the first term and d is known as the common difference.
The common difference can be found by subtracting the second term - first term.
That would be: 4 - -2 = 4 + 2 = 6
So the common difference (d) of this sequence is 6.
We also know that the first term is -2.
Now, we can find the next three terms.
The third term will be:
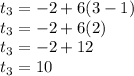
The fourth term will be:
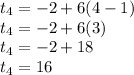
The fifth term will be:
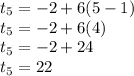
So the next three terms will be: 10, 16, and 22.