The Pythagoras theorem says that the sum if a right triangle has side length a, b, and c then
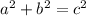
Now in our case, a = 8, b = ?, and c = 16 in; therefore,
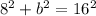
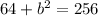
Subtracting 64 from both sides gives
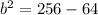
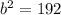
Taking the square root of both sides gives
![b=\sqrt[]{192}](https://img.qammunity.org/2023/formulas/mathematics/college/zlztviprfqyukvylyafj3ibh2fa6q8f17r.png)
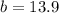
Hence, the length of the missing side is 13.9.