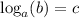
Using the definition of the base of a log:
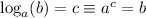
According to this, c could be a negative number, here's why:
Let's try to find the following logarithm:
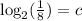
Using the definition of the base of a log:
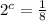
We can express 8 as 2³:
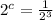
Using the following property:
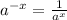
We can express the equation as:
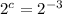
From this, we can conclude that c = -3, therefore it is possible for x to equal a negative number.