Question

I will send a picture. Thanks

Answer 1

We need to form a polynomial with degree 3

And zeros = 1 + i and -9

So, one of the root is complex,

so, the other will be the conjugate of the given

So, the roots will be : (1 + i) , ( 1 - i) and (-9)

Multiplying the roots together will give minues the the absolute coefficient

So,

`\begin{gathered} (1+i)\cdot(1-i)\cdot(-9) \\ =\lbrack(1+i)\cdot(1-i)\rbrack\cdot(-9) \\ =(1-i^2)\cdot(-9) \\ =(1-(-1))\cdot(-9) \\ =(1+1)\cdot(-9) \\ =2\cdot(-9)=-18 \end{gathered}`

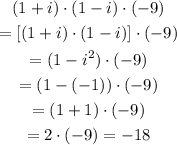
so, the absolute coefficient = 18

So, the answer is option 3 or 4

(x + 9) and ( x - [1+i] ) and ( x - [1-i] )

Multiplying the last two roots

`\begin{gathered} (x-\lbrack1+i\rbrack)(x-\lbrack1-i\rbrack) \\ =(x-\lbrack1+i\rbrack)\cdot(x+\lbrack i-1\rbrack) \\ =(x^2-2) \end{gathered}`

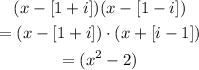
So, the absolute coefficient =