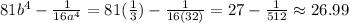Question

If a^4=32 and b^4=1/3 find the value of(3b-(1/2a))(3b+(1/2a))((1/4a^2)+9b^2)

Answer 1

You have the following expression:

`(3b-(1)/(2a))(3b+(1)/(2a))((1)/(4a^2)+9b^2)`

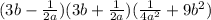
if a⁴ = 32 and b⁴ = 1/3, and you take into account that the product between the first two factors is a difference of squares, you obtain:

`\begin{gathered} (3b-(1)/(2a))(3b+(1)/(2a))((1)/(4a^2)+9b^2) \\ =(9b^2-(1)/(4a^2))((1)/(4a^2)+9b^2) \\ =(9b^2-(1)/(4a^2))(9b^2+(1)/(4a^2)) \end{gathered}`

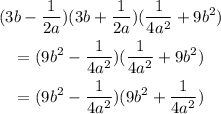
Where you have used that (a + b)(a - b) = a² - b². The last result is again a difference of square, then you have:

`\begin{gathered} (9b^2-(1)/(4a^2))(9b^2+(1)/(4a^2)) \\ =(81b^4-(1)/(16a^4)) \end{gathered}`

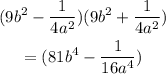
Finally, you replace the given expressions for a and b:

`81b^4-(1)/(16a^4)=81((1)/(3))-(1)/(16(32))=27-(1)/(512)\approx26.99`