Question
An octagon has a side length of 18 feet and an area of 806.4 ft^2
Find the area of a smaller octagon that has a side length of 15 feet
Answer:
Explanation:
We are given two octagons in the above question.
Side length of larger octagon = 18 feet
Area of larger octagon = 806.4 ft^2
The area of a smaller octagon = X
Side length of smaller octagon = 15 feet
We solve for this using scale factor
Scale factor(k) = ratio of the side length of the octagon = smaller side length/ larger side length
k = 15/18
It is important to note that
The square of the scale factor k = ratio of the areas of the octagon
Hence,
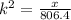
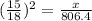

Cross Multiply
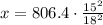
x = 560 ft^2