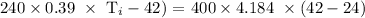Answer:
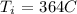
Step-by-step explanation:
Here, we want to get the initial temperature of the copper piece
Mathematically:
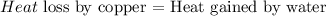
The amount of heat lost or gained by any substance can be calculated as:
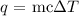
where:
m represents the mass
c represents the specific heat capacity (heat capacity of water is 4.184 J/g.C)
delta T represents the temperature change
Substituting the values, we have it that: