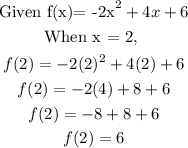
To find the maximum of the function:
From the graph, the maximum occurs at x = 1
We can also confirm using gradient at turning point idea to establish that the maximum of the function occurs at x = 1

Substituting x= 1 into f(x), we have
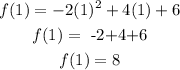
The maximum is 8