Question

Fill in the P(X = x) values in the table below to give a legitimate probability distribution for the discrete random variable X, whose possible

Answer 1

• P(X=2) = 0.25

,

• P(X=5) = 0.25

Explanation:

A probability distribution must satisfy the following two conditions.

• P(X=x)≥0 i.e. it must be non-negative.

,

• The sum of P(X=x) must always be 1.

From the data given in the table, let the probabilities:

• P(X=2) = x

,

• P(X=5) = x

In order for the table to give a legitimate probability distribution, the sum of P(X=x) must be 1. Therefore:

`\begin{gathered} 0.12+0.26+0.12+x+x=1 \\ 0.5+2x=1 \\ 2x=1-0.5 \\ 2x=0.5 \\ x=(0.5)/(2) \\ x=0.25 \end{gathered}`

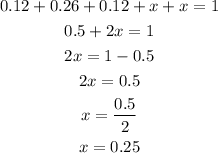
Thus, if the two empty columns are filled with 0.25 each, the table is a valid probability distribution.

Note: Any other two values can be used provided that they add up to 0.5