Question

The volume of a rectangular prism is 2x3 +17x2 +38X + 15 and one side has a length of x + 5. FInd thelength of one of the other sides.

Answer 1

Polynomial Division

This problem requires finding the division of two polynomials. Let's get into the details.

The volume of a rectangular prism of dimensions W, L, and H is given by:

`V=W\cdot L\cdot H`

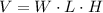
If we were given the volume and one of its sides, say W, we can find the product of the other sides (L and H) by solving the equation:

`L\cdot H=(V)/(W)`

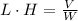
We know the value of the volume as a polynomial and the value of one side as a polynomial also:

`L\cdot H=(2x^3+17x^2+38x+15)/(x+5)`

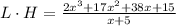
This means to find LH we need to divide the polynomials as given. Since the polynomial in the denominator is a binomial with a leading coefficient of 1, we can divide faster and easier by using the synthetic division.

We collect the coefficients of the dividend when ordered by decreasing degree. These coefficients are 2, 17, 38, and 15.

Then we set up the method as follows:

| 2 17 38 15

-5 |

|-----------------------

The number -5 is the independent term of the denominator with its sign changed.

Now we drop the first coefficient to the last row and multiply by -5:

| 2 17 38 15

-5 | -10

|-----------------------

2 7

Note we operated 17 - 10 = 7

Now we multiply again by -5:

| 2 17 38 15

-5 | -10 -35 -15

|-----------------------

2 7 3 0

Repeating the procedure, we find the last term is 0. That number corresponds to the remainder of the division. Recall a remainder zero means the division is exact.

The three remaining coefficients are 2, 7, and 3. They form a new polynomial of degree 2.

Going back to our division we have:

`L\cdot H=2x^2+7x+3`

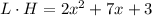
Note we have found the product of the two other sides, be we cannot know the length of one of them individually, just their product.