Question

Two cars start out at the same spot. One car starts to drive North at 18 mph 5 hours before the second car starts driving to the East at 48 mph. How long after the first car starts driving does it take for the two cars to be 300 miles apart? (straight line distance, as the crow flies)

Answer 1

10 hours

Step-by-step explanation:

The first car drives North at 18mph for 5 hours.

Distance=Speed X Time

Therefore, the distance covered by the first car in x (x>5) hours will be:

`Dis\tan ce=18x\text{ miles}`

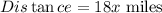
The second car starts driving to the East at 48 mph.

The second car would have been driving for (x-5) hours.

Therefore, the distance covered by the second car in x-5 (x>5) hours will be:

`Dis\tan ce=48(x-5)\text{ miles}`

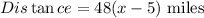
The straight line distance (hypotenuse) between the two at x hours = 300 miles

Applying Pythagoras theorem, we have that:

`(18x)^2+\lbrack48(x-5)\rbrack^2=300^2`

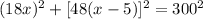
We solve the equation derived above for x.

`\begin{gathered} 324x^2+2304(x-5)(x-5)=90000 \\ =324x^2+2304(x^2-5x-5x+25)=90000 \\ =324x^2+2304(x^2-10x+25)=90000 \\ \implies324x^2+2304x^2-23040x+57600-90000=0 \\ \implies2628x^2-23040x-32400=0 \end{gathered}`

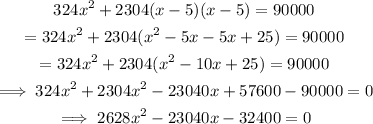
We can then solve using the quadratic formula:

`\begin{gathered} x=(-b\pm√(b^2-4ac))/(2a) \\ a=2628,\text{ b= - 23040, c=-32400} \\ x=(-(-23040)\pm√((-23040)^2-(4*2628*-32400)))/(2*2628) \\ =(23040\pm29520)/(5256) \\ x=(23040+29520)/(5256)\text{ or }(23040-29520)/(5256) \\ x=10\text{ or -1.23} \end{gathered}`

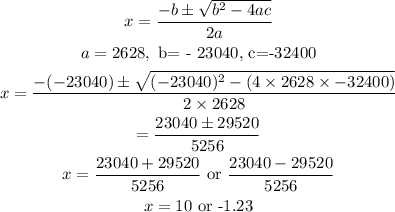
Since time cannot be negative

x=10 hours

Therefore, 10 hours after the first car starts driving, the two cars are 300 miles apart.