Question

How much heat is needed to melt 10.0 grams of ice at -10°C until it is water at 10°C?Group of answer choicesA. +83.6 JB. +3963 JC. -3963 JD. -83.6 J

Answer 1

3,961J are needed. (The closest option is B. +3963J).

Step-by-step explanation:

The given information from the exercise is:

- Mass of water: 10.0g

- Initial temperature of ice: -10°C

- Final temperature of water: 10°C

To calculate the heat of each parte of the melting process, it is also necessary to use the following information:

- Heat of fusion (hf): 334 J/g

- Specific heat capacity of ice (ci): 2.03 J/g.°C

- Specific heat capacity of water (cw): 4.18 J/g.°C

To calculate the total heat of the melting process, it is necessary to calculate 2 types of heat:

• (Q1) Heat needed to raise the temperature of ice from -10°C to 0°C:

`\begin{gathered} Q_1=m*c_i*\Delta T \\ Q_1=m*c_i*(T_f-T_i) \\ Q_1=10.0g*2.03\frac{}{g\degree C}*(0\degree C-(-10\degree C)) \\ Q_1=203J \end{gathered}`

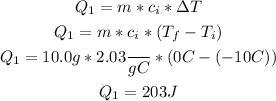
• (Q2) Heat required to transform the entire mass of ice into water:

`\begin{gathered} Q_2=m*hf \\ Q_2=10.0g*334(J)/(g) \\ Q_2=3,340J \end{gathered}`

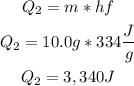
• (Q3) Heat needed to raise the temperature of water from 0°C to 10°C:

`\begin{gathered} Q_3=m*c_w*\Delta T \\ Q_3=m*c_w*(T_f-T_i) \\ Q_3=10.0g*4.18(J)/(g\degree C)*(10\degree C-0\degree C) \\ Q_3=418J \end{gathered}`

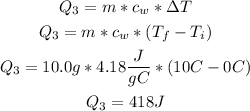
Finally, we have to add each heat value (of each part of the process), to calculate the total heat needed:

`\begin{gathered} Q_T=Q_1+Q_2+Q_3 \\ Q_T=203J+3,340J+418J \\ Q_T=3,961J \end{gathered}`

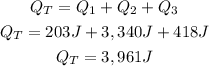
So, 3,961J are needed. (The closest option is B. +3963J).