To calculate the volume of this figure, we just have to find the volume of the hemisphere and the volume of the cone, then sum them up.
The volume of a hemisphere (the half of a sphere) is given by the formula:
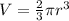
Where r is the radius.
The volume of a cone is given by the formula:
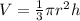
Where h is the height of the cone.
From the figure we have:
r = 5.3in
h = 9 in
Then, when we substitute these values into the above formulas, we get:
For the hemisphere:
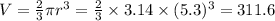
The volume of the hemisphere is 311.6in^3
For the cone:
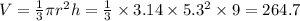
As mentioned, the volume of the whole figure is the sum of the volume of the cone and the volume of the hemisphere, then, the volume of the figure is:
V=311.6in^3 + 264.7in^3 = 576.3in^3
Then, the correct answer is option A