Question

From his eye, which stands 1.52 meters above the ground, Wyatt measures the angle of elevation to the top of a prominent skyscraper to be 28∘. If he is standing at a horizontal distance of 331 meters from the base of the skyscraper, what is the height of the skyscraper? Round your answer to the nearest tenth of a meter if necessary.

Answer 1

Given:

The angle of elevation from a distance of 1.52 meters above the ground = 28

he is standing at a horizontal distance of 331 meters from the base of the skyscraper

Let the height of the skyscraper = h

So, we will find (h) as follows:

`\begin{gathered} tan(28)=(h-1.52)/(331) \\ \\ h=331*tan(28)+1.52 \end{gathered}`
`h=177.5158`

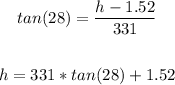
Rounding to the nearest tenth

So, the height of the skyscraper = 177.5 meters