Question

I have this practice sheet and i am unsure how to solve yhis problem

Answer 1

Now, we know that in order to get 85% of the original height, we have to multiply it by 0.85

`15\cdot0.85`

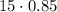
Now, we can do this for every bounce, and calculate the final height by adding an extra 0.85

`15\cdot0.85\cdot0.85\cdot0.85\cdot0.85\ldots`

If we were to calculate the final height of the third bounce, we would have to use 0.85 three times, as following:

`15\cdot0.85\cdot0.85\cdot0.85=9.2`

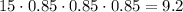
Therefore, the ball would end up at 9.2 feet after the third bounce

Answer: Option A