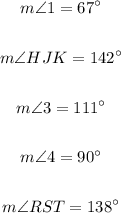Question

How is this done I’m trying to help my son

Answer 1

To answer this question, we need to remember that when two parallel lines are cut by a transversal, the following pairs of angles are congruent (they have the same measure):

• Alternate interior angles

,

• Corresponding angles

,

• Alternate exterior angles

We also need to remember that two consecutive interior angles are supplementary, that is, their sum is equal to 180 degrees.

Having this information into account, we can proceed as follows:

Case 1:

We have here two corresponding angles, <1 and 67°. We can see that these angles lie on the same side of the transversal T, and one of the angles lies on the interior of the parallel lines (67°) and the other lies on the exterior of the parallel lines (<1).

Therefore, we can say that <1 and 67 are congruent, and then:

`m\angle1=67^(\circ)`

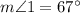
Case 2:

We also have here two corresponding angles, and we have that:

`\begin{gathered} m\angle HJK=x^(\circ) \\ \\ m\angle HJK=142^(\circ) \end{gathered}`

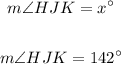
Case 3:

In this case, we have alternate interior angles, and because of that, the angles are also congruent:

Therefore, we have:

`m\angle3=111^(\circ)`

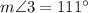
Case 4:

In this case, we have two consecutive interior angles, and we know that one of them is a right angle - we can see a small square. Since we have the sum of two consecutive interior angles is equal to 180° (they are supplementary angles), then we have:

`\begin{gathered} m\angle4+90^(\circ)=180^(\circ) \\ \end{gathered}`

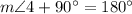
To solve this equation, we need to subtract 90° from both sides of the equation:

`\begin{gathered} m\angle4+90^(\circ)-90^(\circ)=180^(\circ)-90^(\circ) \\ \\ m\angle4=90^(\circ) \end{gathered}`

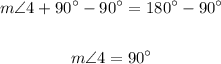
Case 5:

In this case, we have two alternate exterior angles, as we can see in the next drawing:

Therefore, we have that:

`m\angle RST=138^(\circ)`

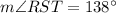
In summary, therefore, we have that:

`\begin{gathered} m\angle1=67^(\circ) \\ \\ m\angle HJK=142^(\circ) \\ \\ m\angle3=111^(\circ) \\ \\ m\angle4=90^(\circ) \\ \\ m\angle RST=138^(\circ) \end{gathered}`