Given:
Probability that Brandon reaches the base = 0.38
Probability that Francisco reaches the base = 0.34
Probability that Pete hits a homerun = 1/12 or 0.0833
So, the chances that Brandon and Francisco both reach the base, followed by Pete hitting a home run to win the game is:
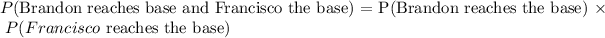
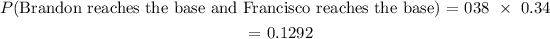
![\begin{gathered} P(\text{Brandon reaches the base and Francisco reaches the base, followed by Pete hitting a homerun) } \\ \text{ = }P(Brandon\text{ reaches the base and Francisco reaches the base) }*\text{ }P(Pete\text{ hits a homerun)} \\ =\text{ 0.12}92\text{ }*\text{ 0.0833} \\ =\text{ 0.010766 } \\ =\text{ 1.0766\%} \\ =\text{ 1.08\% (nearest tenth of a percent)} \\ \\ \end{gathered}]()
Hence the solution to the problem is 1.08%