1 Answer

Edwing · Answer 1 · 2023-08-17T08:57:18+0000

To determine the length of the arc, we first solve the circumference of the circle using the formula C = 2πr.

Based on the circle, its radius is 6 cm.

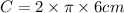
$C=2*\pi*6cm$
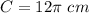
$C=12\pi\text{ }cm$

Therefore, its circumference is 12π cm.

Next, we multiply the circumference by the ratio of its intercepted central angle and the 1 whole revolution.

In this case, the ratio is 120°/360°

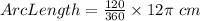
$ArcLength=(120)/(360)*12\pi\text{ }cm$
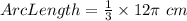
$ArcLength=(1)/(3)*12\pi\text{ }cm$
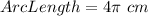
$ArcLength=4\pi\text{ }cm$

Therefore, the length of arc MN is 4π cm. (Option 4)

Please log in or register to add a comment.