Question

graph the proportional relationship D=60t that expresses your distance traveled in D (miles) in terms of time t (in hours) since you started going 60 mph

Answer 1

The equations for Proportional relationships have the following form:

`y=kx`

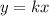
Where "k" is the Constant of proportionality.

By definition, the graph of Proportional relationships is a line that passes through this point:

`(0,0)`

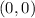
This is called "The origin".

As you can notice, this is the same as write the Equation of a line that passes through the Originl, where "m" is the slope of the line:

`y=mx`

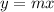
In this case you have:

`D=60t`

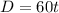
So, in order to graph the Proportional relationship, you can give values to "t" in order to find points on this line. Then:

1. When:

`t=2`

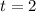
You get:

`D=60(2)=120`

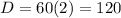
So you have the point:

`(2,120)`

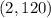
2. When:

`t=4`

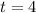
You get:

`D=60(4)=240`

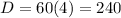
The point is:

`(4,240)`

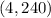
Plot the points on the Coordinate plane. The line must pass through them.

Therefore, the graph of this Proportional relationships is: