Question

Find equation of the line which passes through the point (4,3) and is perpendicular to the line with the equation Y = 1/2 X -5 express your answer in slope intercept form simplify your answer

Answer 1

Equation of a line in slope-intercept form is given as

`\begin{gathered} y=mx+b \\ where\text{ m = slope and b = y-intercept } \end{gathered}`

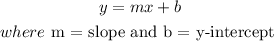
comparing this to the equation

`\begin{gathered} y=(1)/(2)x-5 \\ the\text{ slope of this line m = }(1)/(2) \end{gathered}`

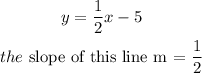
For two lines that are perpendicular, the peroduct of their slope = -1, so

`\begin{gathered} m_1m_2=-1 \\ (1)/(2)m_2=-1 \\ m_2=-1/(1)/(2) \\ =-1*(2)/(1) \\ =-2 \end{gathered}`

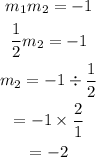
So the slope of this other line is -2. This line passes through the point (4, 3)

the equation of this line becomes

`\begin{gathered} y-y_1=m(x-x_1) \\ y-3=-2(x-4) \\ y-3=-2x+8 \\ y=-2x+8+3 \\ y=-2x+11 \end{gathered}`

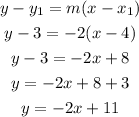
Hence the answer is

y = -2x + 11