Question

At a movie theater, child admission is $5.80 and adult admission is $9.00. On Saturday, 132 tickets were sold for a total sales of $960.80. How many child tickets were sold that day?

Answer 1

We need to find the number of child tickets sold that day.

We know that child admission is $5.80 and adult admission is $9.00.

Let's call x the number of child tickets and y the number of adult tickets sold that day.

Since 132 tickets were sold, we have:

`x+y=132`

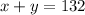
Also, they were sold for a total sales of $960.80. Thus, we have:

`5.8x+9y=960.8`

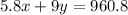
Then, we can isolate y in the first equation, then write its expression in terms of x in the second equation. We obtain:

`\begin{gathered} x+y-x=132-x \\ \\ y=132-x \end{gathered}`
`\begin{gathered} 5.8x+9(132-x)=960.8 \\ \\ 5.8x+1188-9x=960.8 \\ \\ (5.8-9)x+1188-1188=960.8-1188 \\ \\ -3.2x=-227.2 \\ \\ (-3.2)/(-3.2)x=(-227.2)/(-3.2) \\ \\ x=71 \end{gathered}`

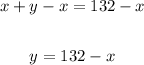
Answer: The number of child tickets sold was 71.