1 Answer

Nuramon · Answer 1 · 2024-01-01T07:03:48+0000

SOLUTION

We want to find the standard deviation of the data in the picture

So we need to make a table

The formula is given as

$\sqrt[]{\sum^{}_{}(x-\operatorname{mean})^2.P(x)}$

So we need to make a table for

$\begin{gathered} x-\operatorname{mean} \\ \text{This is given as } \\ (x-x(Px) \end{gathered}$

Then we square it and multiply for by P(x)

This means we need a table for

$(x-\operatorname{mean})^2.P(x)$

Then we sum and get the square root.

The table is shown below

So the last column is

$\begin{gathered} (x-xP(x))^2.P(x) \\ It\text{ is the same as } \\ (x-\operatorname{mean})^2.P(x) \end{gathered}$

So let us sum

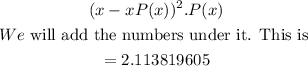
$\begin{gathered} (x-xP(x))^2.P(x) \\ We\text{ will add the numbers under it. This is } \\ =2.113819605 \end{gathered}$

The standard deviation becomes

$\begin{gathered} S\mathrm{}D=\sqrt[]{2.113819605} \\ S\mathrm{}D=1.453898 \end{gathered}$

Hence the answer is 1.45 to 2 decimal places

Please log in or register to add a comment.