Given a set of points (x,y) the line of best fit is given by the least squares method. According to this method the equation of this line is:
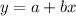
Where a and b are given by:
There are a few quantities to note here. First we have the mean values of x and y:
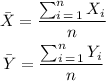
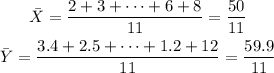
Where Xi and Yi are the x values and y values given by the table and n is the total number of points (x,y). So first of all let's find these two values. We just need to sum all the x values and divide them by 11 (the total amount of points) and then do the same for the y values. Then we get:
Now let's calculate the denominator of b. We need to find this expression for each value of x:
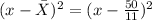
And then add all the results. If we do this for each x value we get the following set of values:
The denominator is given by their sum And this is equal to 24.7273.
For the numerator of b we first need to find:
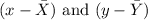
For each x and y. Remember that:
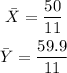
Then we have the following table of values:
The sum of all this values is the numerator of b and it's equal to 30.1273. Then b is equal to:
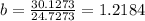
Then a is:
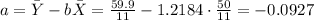
So the slope of the line of best fit is given by b and is equal to 1.2184.
The slope tells us how much does the the y value increases when the x value increases in 1 unit. In this case since x represents the number of people in a household and y represents the pounds wasted the slope represents the food waste per additional person i.e. the amount of food wasted by a person on average. So this is basically saying than a person on average wastes 1.2184 pounds of food per day which seems to be a little high.