Question

X y w z is a quadrilateral with verticals W 1 - -4 - x - -4

Answer 1

Midpoint formula

We are given the points

X=(-4,2)

Y=(1,-1)

Z=(-2,-3)

W=(1,-4)

They define the quadrilateral XYWZ

To find the intersection of the diagonals, we can use the Midpoint Formula

This formula gives us the midpoint of a segment defined by points (x1,y1) (x2,y2) as follows:

`xm=(x1+x2)/(2),\text{ ym=}(y1+y2)/(2)`

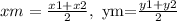
We must identify the opposite points of the quadrilateral and calculate the midpoint between them

Segment XY:

Midpoint of XY:

`x_m=(-4+1)/(2)=-(3)/(2)`
`y_m=(2-1)/(2)=(1)/(2)`

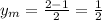
Midpoint of ZW:

`x_m=(1-2)/(2)=-(1)/(2)`
`y_m=(-3-4)/(2)=-(7)/(2)`

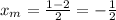
Finally, find the midpoint of the opposite sides' midpoints:

`x_c=(-(3)/(2)-(1)/(2))/(2)=-1`
`y_c=((1)/(2)-(7)/(2))/(2)=-(3)/(2)`

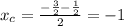
The intersection of the diagonals is the point (-1,-3/2)