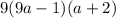We need to facto the trinomial:

Notice that the first term can be factored as:
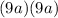
Thus, one possible way of factoring the trinomial is:
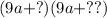
When we multiply the terms represented by "?" and "??", we need to obtain -18. Thus, we need to factor -18 and try each pair of possible factors.
We have:
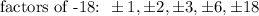
Notice that:
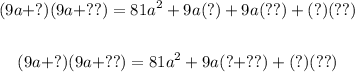
Then, the pair of factors of -18 must satisfy:
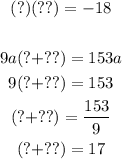
One possible pair of factors of -18, whose sum is 17, is: -1 and 18.
Using those numbers, we obtain:
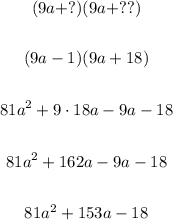
Then, we see that:
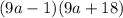
is a way of factoring the given trinomial. Notice, though, that terms of the second factor can both be divided by 9. Then, we can write the expression as:
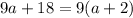
Then, the trinomial can be factored as: