Question

I need some help with this, I'm not sure if is 21 mm because I used the pyg theorem and found the C was 10.5 mm, just need some more help!

Answer 1

We have 2 right triangles, so we can apply a trigonometric function in order to obtain AC and CD.

If we apply cosine funcion in triangle ABC, we get

`\cos 36=(AC)/(8)`

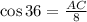
therefore, AC is equal to

`\begin{gathered} AC=8\cdot\cos 36 \\ AC=8\cdot0.809 \\ AC=6.47 \end{gathered}`

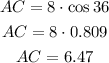
Now, we can apply Pitagorean theorem on triangle ABC in order to find BC, that is

`BC^2+AC^2=AB^2`

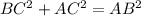
then, we have

`BC\questeq\sqrt[]{AB^2-AC^2}`

If we substitute AB=8 and AC=6.47, we obtain

`\begin{gathered} BC=\sqrt[]{8^2-(6.47)^2} \\ BC=\sqrt[]{64-41.96} \\ BC=\sqrt[]{22.14} \\ BC=4.71 \end{gathered}`

Now, we can draw the following triangle:

So, in order to find CD we can apply Pitagorean theorem again, that is

`\begin{gathered} CD^2+BC^2=BD^2 \\ CD=\sqrt[]{BD^2-BC^2} \end{gathered}`

By substituting the values, we get

`\begin{gathered} CD=\sqrt[]{7^2-(4.71)^2} \\ CD=\sqrt[]{49-}22.1841 \\ CD=\sqrt[]{26.82} \\ CD=5.178 \end{gathered}`

Therefore, the length AD=AC+CD, then the answer is

`\begin{gathered} AD=6.47+5.178 \\ AD=11.65 \end{gathered}`