Note the in such type of questions the term 'probability' and 'proportion' can be used in place of each other. It is because the probability gives the proportion of favorable outcomes to the total outcomes.
Let X be the random variable representing the number of data points greater than or equal to 22.
Given that the mean and standard deviation is 18.5 and 3.25, respectively.
Consider the formula for z-score as,

So the probability is calculated as,
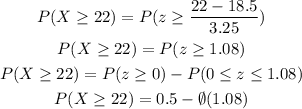
From the Standard Normal Distribution Table,
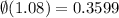
Substitute this value,
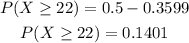
Thus, there is 0.1401 or 14.01% probability that a data will be greater than or equal to 22.
So, the 14.01% of the data is expected to be 22 or greater.