Question

Sketch a graph representing f(x), indicating all intercepts and min or max points.

Answer 1

Explanations:

Given the function below;

`f(x)=4-(x^2)/(8)`

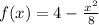
The x-intercept is the point where f(x) = 0 as shown:

`\begin{gathered} 0=4-(x^2)/(8) \\ 0=32-x^2 \\ x^2=32 \\ x=\pm√(32) \\ x=\pm5.66 \end{gathered}`

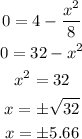
The x-intercept of the graph will be at (5.66, 0) and (-5.66, 0)

The y-intercept occurs at the. point where x = 0 to have:

`\begin{gathered} f(0)=4-(0^2)/(8) \\ f(0)=4 \end{gathered}`

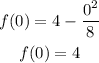
The y-intercept is (0, 4)

The equivalent graphis as shown below

The graph shows that the function has a maxmum point at (0, 4) with no minimum point.