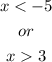Question

The solution set of the quadratic equation x2 + 2x – 15 >O is

Answer 1

To find the set of a quadratic inequation, we first need to find the roots of the quatradic equation. The roots can be found by using the same inequality but changing the inequality sign the euqal sign:

`\begin{gathered} x^2+2x-15>0 \\ x^2+2x-15=0 \end{gathered}`

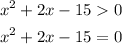
Let's use the Bharkara Equation to find the roots:

`\begin{gathered} x=\frac{-2\pm\sqrt[]{2^2-4\cdot1\cdot(-15)}}{2\cdot1} \\ x=\frac{-2\pm\sqrt[]{4+60}}{2} \\ x=\frac{-2\pm\sqrt[]{64}}{2} \\ x=(-2\pm8)/(2) \\ x=-1\pm4 \\ x_1=-1+4=3 \\ x_2=-1-4=-5 \end{gathered}`

So we get the roots x = 3 and x = -5. This are the point at which the graph changes its sign.

The quadratic term (the one multiplying x²) is 1, which is positive. Because of that, the parabola of the quadratic expression has a minimum vertex:

For the drawing, it can be seen that when x is between -5 and 3, the equation has a negative sign, while when x is lower than -5 or greater than 3 the expression has positive sign. We want the expression:

`x^2+2x-15>0`

So, when it is greater than 0, meaning positive. Then, the set that solves the quadratic inequation is:

`\begin{gathered} x<-5 \\ or \\ x>3 \end{gathered}`