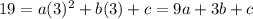Problem
A quadratic function has the form y=ax^2 + bx + c, in which a, b and c are specific numbers and a does not equal 0. Three distinct points on the graph are enough to determine the equation. Suppose that (1,5), (2,10) and (3,19) are on the graph of y =ax^2 + bx + c. Write a system of three variables and three equations.
Solution
For this case we can find the 3 equations on this way:
(x=1, y=5)
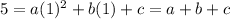
(x=2, y=10)
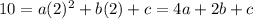
(x=3, y=19)