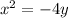Question

Find the equation of a parabola with a focus of (0, -1) and directrix y = 1

Answer 1

For this case we see that the focus is (0,-1)

And the directrix is y=1

So then we have a parabola that open downwards:

The vertex is given by V= (h,k)

The focus is given by: F = (h, k+p)

And the directrix is given by: y= k-p

So then replacing we got:

1 = k-p (1)

h = 0

k+p = -1 (2)

Using equation (1) we got k:

k = p+1

Replacing into second equation we got:

p+1+p = -1

2p = -2

p= -1

k = -1 +1= 0

Then the vertex is given by: V= (0, 0)

And the formula is given by:

`(x-0)^2=4(-1)(y-0)`

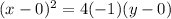
And thats equivalent to :

`x^2=-4y`