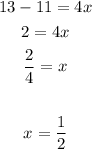A function is a relation in which each input value (x-value) has one and only one output value (y-value).
You have the following Linear function:
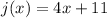
According to the explained in the problem, you must find an input value that gives you 13 as the output value. Knowing this, you can say that:
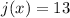
Substitute this value into the given function:
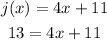
The final step is to solve for "x".
Therefore, the value of "x" so that the function has the given value 13, is: